发文 | Kasper Müller
汉语翻译 | Nothing
校审 | zhenni

海森堡
我常常听见大家讲,是由于观测者根据光量子和电子产生相互影响使光量子的动量矩受到了危害,所以才导致了海森堡不确定性原理。
观测者务必根据危害电子器件的动量矩(或一些量子态)来查看它,这也许是真的,但这不是造成不确定性原理的真实缘故!
在逐渐探讨这一话题讨论以前,使我们先界定海森堡不确定性原理(Heisenberg’s uncertainty principle)。
在电磁学中,存有一系列有关共轭点参量(如部位和动量矩)的基本不等式,他们限制了与此同时精确测量这种成双参量的精密度,这种基本不等式中的任意一个都能够被称作不确定性原理(或者海森堡不确定性原理)。
——维基百科
一种常用的描述方法是,在任意给出的时间点,你都没法与此同时准确地精确测量粒子的角动量和部位。
这类可变性不在于设施的优劣,也不是因为难以清除数据误差。不管大家做得多么好,大家都没法与此同时精确测量这两个量(如动量矩和动能)……
最先,存有许多种不确定性原理,在其中许多能在宏观世界中见到。即使你并没有意识到他们的存有,但其实也一直在和这种状况相处。
次之,海森堡不确定性原理身后与数学课拥有密切的关系。
全部波和化学物质(共轭点自变量)都务必遵循一系列的不确定性原理,真真正正导出来这种基本原理的是一个数学课客观事实(稍候详细描述)。
歌曲、雷达技术、新能源技术跟光也是有务必遵循的“不确定性原理”,大家很快就会见到,是数学确定了这一切。
波
一切都能够归结为十分简单的事情。不管多繁杂的的数据信号或函数公式,事实上全是正弦波形的累加。正弦波形是具备特殊光波长和波幅的波。
累加只是代表着所有的波相互影响,全部波的和(称之为干预)便是组成更繁杂数据信号的累加。
换句话说,大家可以将一个函数溶解为构成它的更简单的一部分(正弦波形)。这基本上就是我们在预估傅里叶级数的傅立叶指数时所需做的一切。非常值得的一提的是,这个方法针对非函数周期一样可用。
这类实际效果在音乐中是众所周知的,比如,吉它生中的泛音会影响主波(弦的工作频率)。换句话说,吉它的响声(或者其他别的传统乐器,包含你的声誉)是由工作频率和震幅不一样的正弦波形构成的。
在我们叙述那样一个繁杂的信息时,大家有二种等额的的方法可以选择。换句话说,我们可以挑选2种不一样的企业对它进行叙述。
我们可以挑选用的时间来叙述造成干预样图的全部波是如何与此同时相互影响的,也能够挑选用组成干预样图的正弦函数波的频率来表述它。
可以用二种等效电路的方法来表述的情况被称作双向关联(dual relationship)。
假如我们可以找到一个数学软件来叙述时长数据信号和频率信号中间的双向相互关系,那自然最好不过。实际上,大家的确找到这种专用工具。
傅里叶变换
我上边谈及的叙述这类双向关联的设备称为傅里叶变换(Fourier transform)。不容置疑,这是数学软件中最强劲、最常用的工具之一。
在得出它的一些特性以前,大家先讲一讲这类傅里叶变换的一些一般特性:
傅里叶变换是一种积分变换(也就是一个算符),它取得一个函数并回到另一个函数。
做为函数公式室内空间上的一个算符,我们可以把它看作是纯数学的行为主体,但我们可以授予它非常好的物理化学表述。在物理和数学行业,我们都可以应用它。
今日,大家关键将从物理学的视角来考虑到它。
在接下来的探讨中,大家假定积分兑换自始至终收敛性。

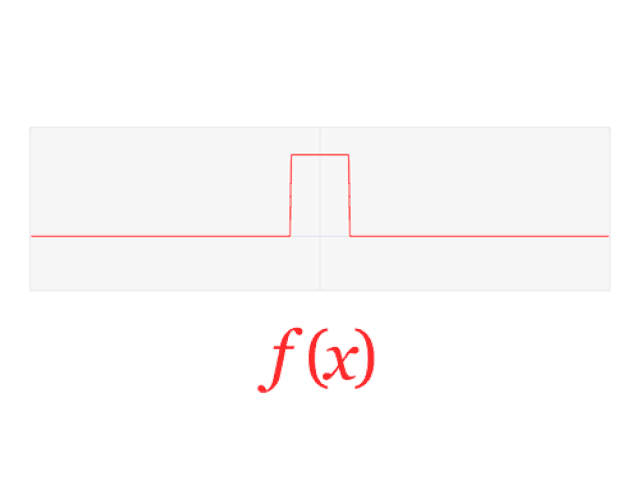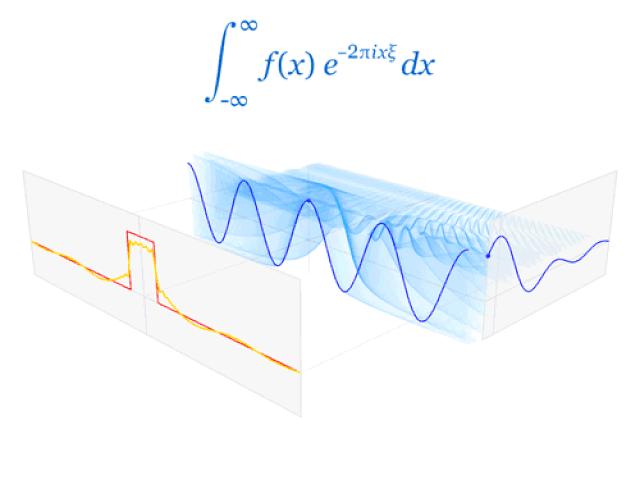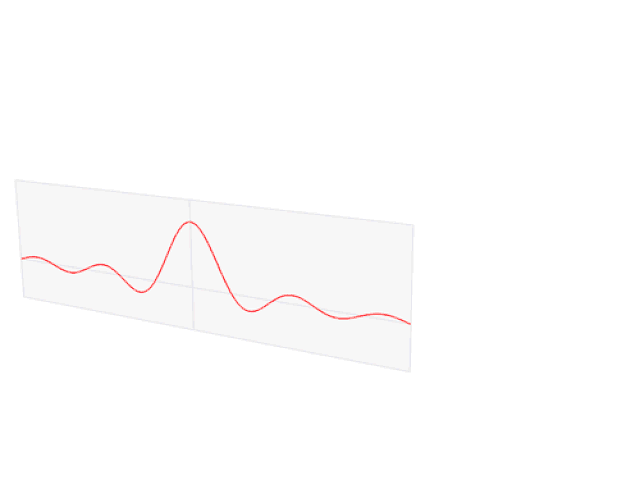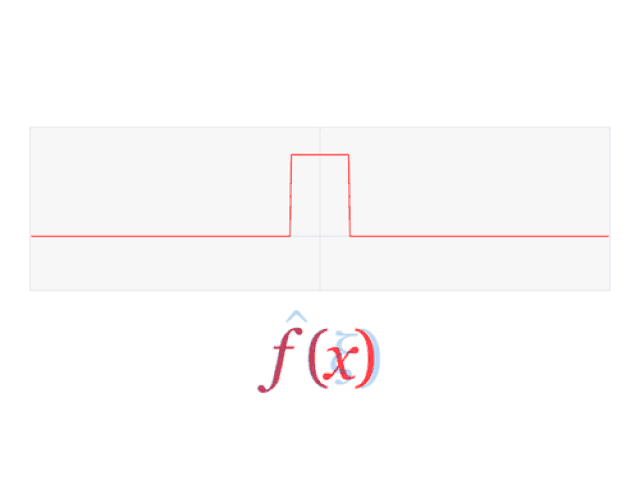
一个差分信号的傅里叶变换是一个sinc函数。全部数据信号都可以用时长或工作频率表明的正弦波来结构丨由来:Lucas Vieira
了解数据信号一直可以用二种等效电路的表达形式是非常重要的。只需给出其中一个,另一个是唯一明确的,大家有一个表达式能够对他们开展测算。如何选择只是在于大家想要什么方式表述一个信号。
唯一的傅立叶逆变换由下列公式计算得到:
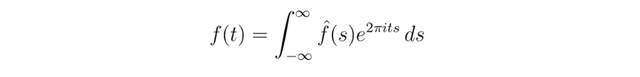
傅里叶变换的特性
傅里叶变换不是一一节课就能够讲明白的,大家只有在这篇文章中讲点毛皮。但是,傅里叶变换的一些令人惊奇的特性是一定要讲的:

进一步大家获得关系式:
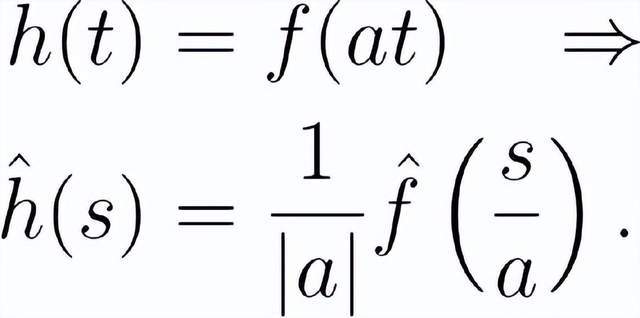
它的物理学意义是什么?
傅里叶变换的平均误差特性代表着,如果我们在时间上缩小数据信号,相当于在工作频率室内空间(水准)上拓展数据信号,相反也是。
大家很快就会发觉,这一结论至关重要。
根据层面进行分析能够给大家给予一个更高端和有创造性的角度。时长以秒为企业考量,工作频率以1/s为企业开展考量。好像可以看出,如果把时长宽化增大,工作频率宽化就会变小,相反也是。
如果你不了解工作频率的企业是从哪里来的,我十分能理解你的困惑。傅里叶变换中的s最后决定了组成信息的正弦波形的周期时间,你可以通过应用欧拉公式将复指数值进行为正弦和余弦,或是将傅里叶变换视作一组持续的傅立叶指数来体会这一点。
傅里叶变换有许多华丽的特性,但因为这不仅仅是一篇关于转换自身的文章内容,我们将但是多详细介绍这种特性,感兴趣的阅读者能够自己来探寻这一点。
阅读者可能会看到一个让测算变简单的特性,即傅里叶变换将求导数变换为乘于一个常量,这是一个有意思且具备实用性的特性。这代表着一个区域中的线性微分方程相匹配于另一个空间中的代数方程。
因而,一些线性微分方程可以通过转换方程式,用解析几何方式求得,随后将解转换回家(根据傅立叶逆变换)得到本来方程的解。
波函数和海森堡不确定性原理
量子科技科学家根据很有可能存在的量子态来叙述量子科技系统软件(比如粒子)。
叙述量子态的函数公式族被称作波函数,以位置坐标为自变量的波函数的模平方米得出了粒子在空间中的概率分布函数。
因而,大家可以将波函数表述为几率波,表明粒子坐落于给出室内空间地区的几率。因而,叙述粒子部位的波函数应当被看作是室内空间中的波而不是时长中的波。
在我们对这个位置波(位置坐标为因变量的波函数)开展傅里叶变换时,能够获得一个工作频率(室内空间中的工作频率)波,这是以粒子动量矩为因变量的波函数。
细心想一想并不奇怪,由于假如你觉得仅是波包或物质波,那样动量矩将由光的频率得出。
大家用γ和来表明这类关联。在其中γ是光波长,h是普朗克常数,p是动量矩,f是工作频率,E是动能。
大家把一个粒子限定在越小的间隔时间内,部位波函数就会越局域网化(被水准压挤)。因为动量矩波函数是部位波函数的傅里叶变换,动量矩波函数将被水准拉申,这代表着动量矩将有更多的可变性。这也是以前提及的傅里叶变换的平均误差特性造成的。
实际上,这就是海森堡的不确定性原理!这里只有傅里叶变换起了功效:
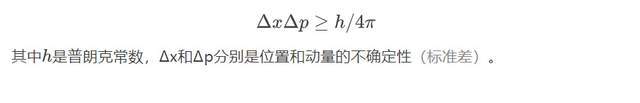
一般的可变性

海森堡不确定性原理仅仅共轭点自变量的例外。
从数学角度看来,为何共轭点自变量的不确定性原理创立?原因是:短消息号,如响声单脉冲,必须很多工作频率不一样的正弦波形的累加才可以完成,仅有很多特殊頻率的正弦波形的累加才可以确保在一定范畴以外波的震幅接近于0。反过来,数据信号越像正弦波形,叙述数据信号需要的次数就会越少。
当你听到很短的一段响声时,你难以明确这一段响声包括什么工作频率;但如果你听到一段不断时间很长的纯粹数据信号,就能划分出不一样的次数。那也是不确定性原理。
一样的,大家对雷达探测器的总体目标的间距了解得越多,对达到或倒退的效率就了解得越少,相反也是。这也是多谱勒和间距的可变性。
也有别的很多共轭点自变量,他们都遵照分别的不确定性原理,两者有一个相同之处,就是他们的建立全是有数学课确保的!波的数学课仅仅限制了我们可以从某一量子态中得到是多少信息内容。
海森堡不确定性原理的危害真实存在
假如你将激光发生器指向间隙,光屏会把一部分光抵抗在外面,针对透过过去的一部分,下面会产生神奇的事情。
光源好像在间隙后边的屏上蔓延起来,假如你让间隙越来越更窄,那样眼会弥漫地更开。这好像和我们的判断力不一致?大家限定它的空间布局,它反倒弥漫着起来。
这一问题是由海森堡不确定性原理造成的。伴随着间隙愈来愈窄,部位波(波函数)愈来愈局域网化(窄),依据不确定性原理,动量矩波函数的宽化越来越大,这导致愈来愈多方位的活动变成很有可能。
因为动量矩是一个有大方向的矢量素材,这代表着光量子在间隙另一侧散播时弥漫的视角越来越越来越大,进而在屏上产生了漂亮的衍射图样。
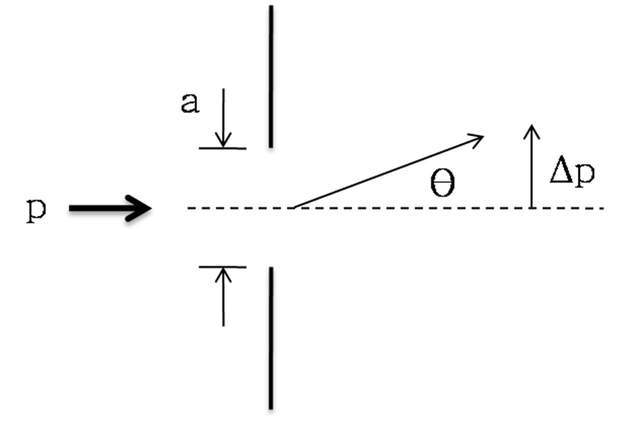
由来:wikimedia
可变性还能够表述为什么太阳会发亮,乃至能够说明为何霍金辐射的时光状况会使超级黑洞变小。
希望有一点确立:可变性是一种单纯的数学课状况,但因为量子科技系统软件让这种数学理论照进现实,因而可变性还可以被当做一种物理原理。
文中经受权转载微信公众平台“中科院物理所”,原文章标题为《不确定原理为啥不确定啊?又被傅里叶懂完了》。
全文连接:
https://www.cantorsparadise.com/heisenbergs-uncertainty-principle-is-pure-mathematics-e14c840659e1
特 别 提 示
1. 进入『返朴』微信公众号底部菜单“精品专栏“,可查阅不同主题系列科普文章。
2. 『返朴』提供按月检索文章功能。关注公众号,回复四位数组成的年份+月份,如“1903”,可获取2019年3月的文章索引,以此类推。